SHORT BIOGRAPHY

I graduated from Polytechnique school, Paris area, in 1995 (X92), did a master of theoretical physics at Ecole Normale Superieure Paris, and moved on to the group of J-L Pichard in Saclay for my PhD (1999). I spent two years as a postdoc in P. Brouwer's group in Cornell University, USA and was hired as a permanent researcher in CEA Saclay in 2002. In 2009, I moved to INAC, CEA Grenoble where I have remained since. You can find almost all my publications here, on arXiv.

OPEN POSITIONS

I don't update this page often enough to advertize the positions here, but I welcome applications at any time. I make a point to answer to all applications (except the generic ones that are sent all over the net). I typically hire one or two postdocs/PhD students every year as well as a couple of master students. If you find the type of research I do interesting, have a good background in theoretical physics, condensed matter and/or nanoelectronics, preferably with some skills with computers, please drop me a line. One of our trademark is that we develop open source codes for solving quantum physics problems, so if you like numerics that are strongly interlinked with the theory, you should really apply.

KWANT, QUANTUM TRANSPORT MADE EASY

When I was a postdoc with Piet Brouwer in Cornell, we had a small piece of code that had been around for a while (I believe the first version was written by Rodolfo Jalabert) and that was so useful that it was called "The Program". "The Program" could essentially calculate the scattering matrix (that gives the conductance) of a small rectangular system connected to two electrodes for an arbitrary confining potential.

KWANT is a software that generalizes "The Program" to a very large class of systems. It works in one, two, three (and even more) dimensions, for an arbitrary mix of lattices (square, honeycomb, amorphous, your pick), arbitrary geometries and internal degrees of freedom (spin, orbitals, superconductivity, etc). It calculates everything we could think of (band structure, scattering matrices, conductances, quantum noise, local density of states, Green's functions, etc). What's more, it is easy to use, you almost write the same Hamiltonian as you would write on the blackboard. KWANT was developped in collaboration with our colleagues at TU Delft.

KWANT is already used by many researchers, both experimenalists and theorists. If you think it could be useful to you, have a look at KWANT web page.

TIME RESOLVED QUANTUM TRANSPORT

We have been developing many techniques that are not yet in the open. One of them is the generalization of KWANT to address time-dependent systems. We are at a very exciting time where high frequency experiments in the quantum regime are moving from the theory papers to actual real experiments. Many concepts from quantum optics (single photon source, interferometers, tomography, etc) start to get their electronics counterpart.

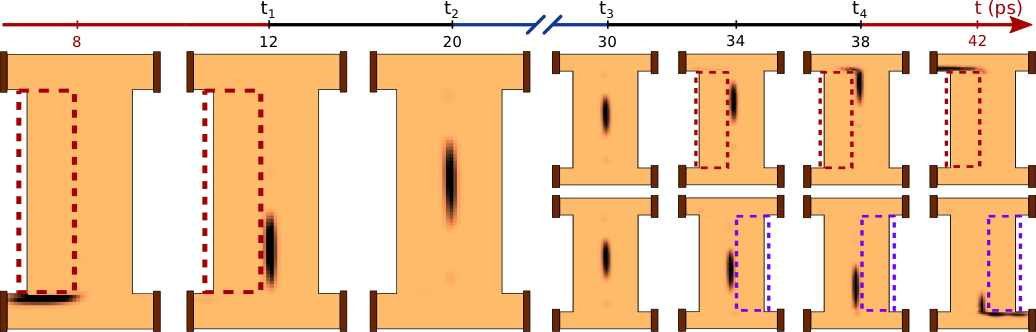
As an illustration, the image below shows a snapshot of a simulation of the propagation of a voltage pulse in the quantum Hall regime: the pulse follows the edge states defined by the electrostatic gates (dashed lines). When the pulse is in the middle, we quickly ground the gate, which freezes the pulse in the middle; we wait a while and then polarize again one of the two gates (red or blue) to restart the pulse toward the upper left or lower right contact. (taken from Phys. Rev. B 90, 161305(R) (2014).

MORE