Atomic disorder in a metal can result in a quantum transition to an insulating state? What happens when the metal is also a superconductor? Spatially resolved tunneling spectroscopy has revealed the spectral signature of this transition in this paradoxical context.

Superconductivity relies on the formation of electron pairs, called Cooper pairs, which condense below Tc in a ground state described by a delocalized electronic wave function, i.e. it extends through the whole sample. The presence of moderate disorder does not fundamentally alter this mechanism, despite scattering effects arising from impurities and material defects. However, if the metal is strongly disordered, quantum interferences associated with the multiple reflections on the defects result in the localization of the electron wave functions. The metallic state is thus changed into an insulating state, a process called Anderson localization.

Superconductivity vs. localization

Physicists very soon understood that this quantum transition should affect the properties of superconducting metals. It is indeed difficult to imagine that the macroscopic spatial extension associated with superconductivity can coexist with the microscopic localization of the electrons. However, several theoretical studies predict that Cooper pairs are less prone to localization than single electrons. As a consequence, some strongly disordered compounds could still exhibit superconductivity and shift to an insulating state only for a higher critical disorder, when Cooper pairs would also localize. Do these Cooper pairs exist for real or only in the wild imagination of some theoreticians? To settle this point, let's observe superconductivity … locally!

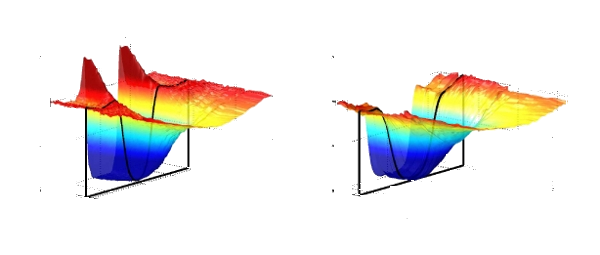
Tunneling spectroscopy to the rescue

The differential conductance between the scanning tunneling electron microscope (STM) tip and the sample surface is proportional to the local density of electronic states. This measurement therefore probes the energy gap of a superconductor in different locations on the surface. Usually, peaks, called coherence peaks, are observed on each side of the gap. We have discovered though that in a strongly disordered superconductor close to the insulating state, amorphous indium oxide, the intensity of the coherence peaks strongly varies with the probed region on the nanometer scale, and that in numerous spectra obtained in the most disordered samples, the peaks were simply absent. The figure shows two thermal dependencies on the density of states for two different samples. In the less disordered sample, the majority of the spectra is similar to the left-hand side panel drawing. For the more disordered one, the right-hand side panel is observed almost everywhere. Based on systematic statistical studies, we have observed a proliferation of peak-less spectra when disorder increases. The disappearance of the coherence peaks is thus correlated to the onset of an insulating state. Numerical simulations and recent theoretical works have confirmed this interpretation. Hundred-year old electron pairs. In 2011, we celebrated the centenary of the discovery of superconductivity, this dramatic property which enables the dissipation-less flow of electrons through some metals when they are cooled below a critical temperature Tc. The rigorously vanishing electrical resistivity was theoretically explained only in 1957 thanks to studies by Bardeen, Cooper and Schrieffer (BCS) who were awarded the Nobel Prize in physics for these results. These researchers realized that electrons need to form pairs in order to superconduct. The formation of pairs, called Cooper pairs, coincides with the disappearance of single electron states and with the opening of a forbidden gap in the density of states. This gap, of width 2 Δ, is characterized by coherence peaks at energies ± Δ.