Les physiciens ont appris qu’en principe une mesure détruit la cohérence quantique. Pourtant, avec une certaine précaution, il est possible de préserver la cohérence voire de manipuler les états quantiques par des mesures.
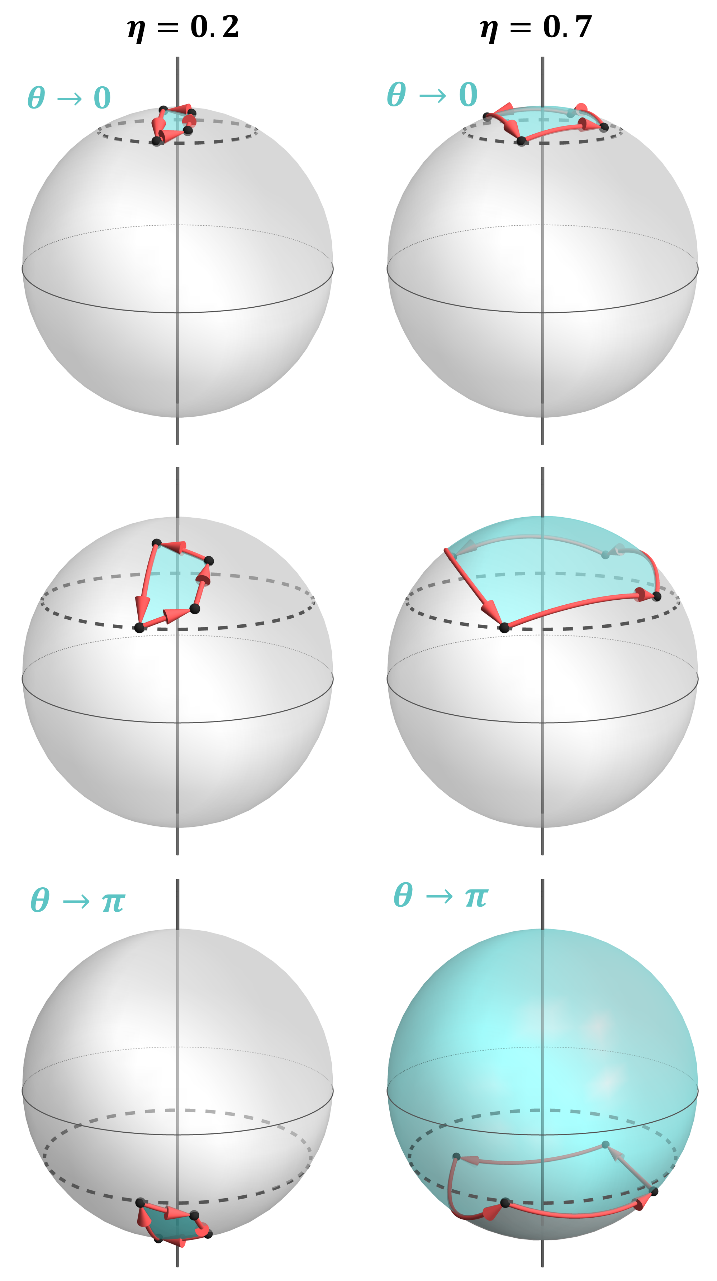
Des chercheurs de PHELIQS/GT [Collaboration] ont étudié comment les mesures quantiques font varier les phases géométriques induites. Ils ont découvert que les phases se comportent de manière topologique radicalement différente selon que les mesures sont faibles ou fortes. Pour des mesures faibles, de force η tendant vers zéro (voir
figure 1 : η=0.2) l’état du qubit est presque identique et présente peu de phase géométrique ; tandis que pour les mesures poussées, de force η tendant vers ∞ (voir
figure 1 : η=0.7) l'état du qubit suit des trajectoires étendues et acquiert une phase géométrique significative. Il s'avère que cette distinction n'est pas seulement quantitative mais peut être qualitative.
Ainsi
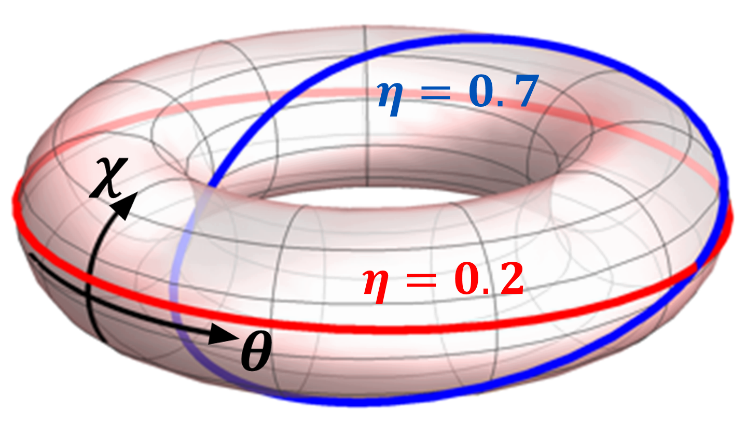
figure 2, la variation de la phase géométrique χ en fonction du paramètre de protocole θ est tracée sur un tore selon les deux coordonnées respectives. La courbe des mesures faibles (en rouge) s'enroule autour du cercle horizontal du tore, mais pas autour du cercle verticla. Tandis que la courbe des mesures fortes (en bleu) s'enroule autour des deux cercles. Il n’est pas possible de passer d’une courbe à une autre par une déformation continue, ce qui les rend distinctes topologiquement. Cela implique nécessairement que la transition entre les deux comportements est abrupte et qu’elle se produit avec une mesure de force intermédiaire.
Les études ont commencé par les études théoriques suivantes :
Récemment, les prédictions ont été confirmées par les expériences suivantes:
Les phases géométriques jouent un rôle important dans la physique quantique des systèmes de matière condensée. Aussi, les propriétés topologiques sont importantes à la fois du point de vue des applications établies (par exemple, le standard de résistance électrique basé sur la conductance de Hall quantifiée topologiquement – appelé Effet Hall quantique, voir dans
Wikipedia) et aussi dans les technologies à venir (Électronique topologique
Communications Physics 2021).
Ces travaux montrent les transitions topologiques induites par la mesure. Et même s’il n’existe pas encore d’applications spécifiques, ces premiers résultats contribuent à une meilleure compréhension des systèmes quantiques en lien avec un environnement perturbant leur cohérence. Cette connaissance peut s'avérer utile, notamment pour éprouver des matériaux réels par des simulateurs quantiques (qui sont soumis à des décohérences/mesures effectuées par leur environnement).
Collaboration : the Weizmann Institute of Science (Israël), University of Freiburg (Allemagne), Lancaster University (RU), Washington University in St. Louis (USA), et University of Ottawa (Canada).